Решето эратосфена с линейным временем работы

Биография[править | править код]

Сын Эглаоса, уроженец Кирены.

Начальное образование Эратосфен получил в Александрии под руководством своего учёного земляка Каллимаха. Другим учителем Эратосфена в Александрии был философ Лизний. Перебравшись затем в Афины, он так тесно сблизился со школой Платона, что обыкновенно называл себя платоником. Результатом изучения наук в этих двух центрах была энциклопедическая эрудиция Эратосфена; кроме сочинений по математическим наукам, он писал ещё трактаты «о добре и зле», о комедии и др. Из всех своих сочинений Эратосфен придавал особенное значение литературным и грамматическим, как это можно заключить из того, что он любил называть себя филологом.

В 245 году до н. э. царь Птолемей III Эвергет пригласил Эратосфена приехать из Афин, чтобы работать в Александрийской библиотеке, где уже трудились его учитель Каллимах и Аполлоний Родосский. Эратосфен откликнулся на приглашение, в возрасте около тридцати лет он приехал в Александрию, где и остался до самой смерти. Через пять лет после приезда он сменил Аполлония Родосского на посту главы Александрийской библиотеки. Как глава библиотеки, Эратосфен занимался обучением детей монарха — будущего правителя Птолемея IV и его сестры (а впоследствии и жены) Арсинои.

На посту главы библиотеки активно занимался её расширением и развитием, стремясь поддержать репутацию библиотеки в соперничестве с Пергамской библиотекой. По его просьбе александрийские портовые власти изымали все книги с приходящих кораблей для изучения и копирования. Эратосфен приобретал аутентичные копии трагедий великих греческих авторов — Эсхила, Софокла и Эврипида, а также учредил в библиотеке целый отдел, занимавшийся изучением творчества Гомера.

В старости у Эратосфена воспалились глаза, что в дальнейшем привело к слепоте. Невозможность читать и наблюдать за природой сильно угнетала его и в 194 год до н. э. он принял решение уморить себя голодом.

Отголоски признания обширной учёности Эратосфена звучат и в прозвищах, которые он получил от современников. Называя его «бета», они, по предположению многих исследователей, желали выразить свой взгляд на него, как на второго Платона, или вообще как на учёного, который только потому занимает второе место, что первое должно быть удержано за предками. Другим прозвищем Эратосфена было «пентатлос» (греч. Πένταθλος) — пятиборец, то есть всесторонне развитый человек, оно было ему дано за одарённость в самых разных областях знания.

В честь Эратосфена назван кратер на Луне, один из периодов геологической истории Луны, а также подводная гора в Средиземном море, близ Кипра.

дальнейшее чтение

• Aujac, Г. (2001). Eratosthene de Cyrène, le pionnier de la géographie . Париж: Издательство CTHS. 224стр.
• Балмер-Томас, Айвор (1939–1940). Избранные, иллюстрирующие историю греческой математики . Кембридж, Массачусетс: Издательство Гарвардского университета.
• Дорофеева А.В. (1988). «Эратосфен (ок. 276–194 до н. Э.)». Мат. В школе (4): I.
• Ельнатанов Б.А. (1983). «Краткий очерк истории развития сита Эратосфена». Истор.-Матем. Исслед. (на русском). 27 : 238–259.
• Фрейзер, PM (1970). «Эратосфен Киренский». Труды Британской академии . 56 : 175–207.
• Фрейзер, PM (1972). Птолемеев Александрия . Оксфорд: Clarendon Press.
• Хонигманн, Э. (1929). Die sieben Klimata und die πολεις επισημοι . Eine Untersuchung zur Geschichte der Geographie und Astrologie in Altertum und Mittelalter. Гейдельберг: Университет Карла Винтера. 247 с.
• Кнаак, Г. (1907). «Эратосфен». Поли-Виссова VI : 358–388.
• Манна, Ф. (1986). «Пентатлос древней науки, Эратосфен, первый и единственный из« простых чисел ». Atti Accad. Понтаниана . Новая серия (на итальянском). 35 : 37–44.
• Muwaf, A .; Филиппу, А.Н. (1981). «Арабский вариант письма Эратосфена о средних пропорциях». J. Hist. Arabic Sci . 5 (1–2): 147–174.
• Никастро, Николас (2008). . Нью-Йорк: Издательство Св. Мартина. ISBN 978-0-312-37247-7.
• Маркотт, Д. (1998). «La Climatologie d’Ératosthène à Poséidonios: genèse d’une science humaine». Дж. Аргу, Дж. Я. Гийомен (ред.). Науки точные и прикладные науки в Александрии (III siècle av JC — Ier ap JC) . Сент-Этьен: Publications de l’Université de Saint Etienne: 263–277.
• Пфайффер, Рудольф (1968). . Оксфорд: Clarendon Press.
• Роулинз, Д. (1982). «Карта Эратосфена — Страбона Нила. Является ли это самым ранним сохранившимся экземпляром сферической картографии? Предоставляла ли она дугу 5000 стадиев для эксперимента Эратосфена?». Arch. Hist. Exact Sci . 26 (3): 211–219.
• Rosokoki, A. (1995), Die Erigone des Eratosthenes. Eine kommentierte Ausgabe der Fragmente , Гейдельберг: C. Winter-Verlag
• Щеглов, Д.А. (2004/2006). «Система семи климатов Птолемея и география Эратосфена». Geographia Antiqua 13 : 21–37.
• Страбон (1917). География Страбона . Гораций Леонард Джонс, пер. Нью-Йорк: Патнэм.
• Таламас, А. (1921). Географ д’Эратостен . Версаль.
• Вулфер, EP (1954). Эратосфен фон Кирена как Mathematiker und Philosoph . Гронинген-Джакарта.

Реализация

Сразу приведём реализацию алгоритма:

int n;
vector<char> prime (n+1, true);
prime = prime1 = false;
for (int i=2; i<=n; ++i)
	if (primei)
		if (i * 1ll * i <= n)
			for (int j=i*i; j<=n; j+=i)
				primej = false;

Этот код сначала помечает все числа, кроме нуля и единицы, как простые, а затем начинает процесс отсеивания составных чисел. Для этого мы перебираем в цикле все числа от до , и, если текущее число простое, то помечаем все числа, кратные ему, как составные.

При этом мы начинаем идти от , поскольку все меньшие числа, кратные , обязательно имеют простой делитель меньше , а значит, все они уже были отсеяны раньше. (Но поскольку легко может переполнить тип , в коде перед вторым вложенным циклом делается дополнительная проверка с использованием типа .)

При такой реализации алгоритм потребляет памяти (что очевидно) и выполняет действий (это доказывается в следующем разделе).

Время работы и требуемая память

Хотя асимптотика лучше асимптотики классического решета Эратосфена, разница между ними невелика. На практике это означает лишь двукратную разницу в скорости, а оптимизированные варианты решета Эратосфена и вовсе не проигрывают приведённому здесь алгоритму.

Учитывая затраты памяти, которые требует этот алгоритм — массив чисел длины и массив всех простых длины примерно — этот алгоритм кажется уступающим классическому решету по всем статьям.

Однако спасает его то, что массив , вычисляемый этим алгоритмом, позволяет искать факторизацию любого числа в отрезке за время порядка размера этой факторизации. Более того, ценой ещё одного дополнительного массива можно сделать, чтобы в этой факторизации не требовались операции деления.

Знание факторизации всех чисел — очень полезная информация для некоторых задач, и этот алгоритм является одним из немногих, которые позволяют искать её за линейное время.

Таблица простых чисел

Простые числа, для удобства их дальнейшего использования, записывают в таблицу, которую называют таблицей простых чисел. Ниже представлена таблица простых чисел до 1 000.

Возникает логичный вопрос: «Почему мы заполнили таблицу простых чисел только до 1 000, разве нельзя составить таблицу всех существующих простых чисел»?

Ответим сначала на первую часть этого вопроса. Для большинства задач, при решении которых придется использовать простые числа, нам будет вполне достаточно простых чисел в пределах тысячи. В остальных случаях, скорее всего, придется прибегать к каким-либо специальным приемам решения. Хотя, несомненно, мы можем составить таблицу простых чисел до сколь угодно большого конечного целого положительного числа, будь то 10 000 или 1 000 000 000, в следующем пункте мы поговорим о методах составления таблиц простых чисел, в частности, разберем способ, получивший название .

Теперь разберемся с возможностью (а точнее с невозможностью) составления таблицы всех существующих простых чисел. Мы не можем составить таблицу всех простых чисел, потому что простых чисел бесконечно много. Последнее утверждение представляет собой теорему, которую мы докажем после следующей вспомогательной теоремы.

Теорема.

Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

Доказательство.

Пусть a – натуральное число, большее единицы, и b – наименьший положительный и отличный от единицы делитель числа a. Докажем, что b – простое число методом от противного.

Предположим, что b – составное число. Тогда существует делитель числа b (обозначим его b₁), который отличен как от 1, так и от b. Если также учесть, что абсолютная величина делителя не превосходит абсолютной величины делимого (это мы знаем из свойств делимости), то должно выполняться условие 1<b₁<b.

Так как число a делится на b по условию, и мы сказали, что b делится на b₁, то понятие делимости позволяет говорить о существовании таких целых чисел q и q₁, что a=b·q и b=b₁·q₁, откуда a= b₁·(q₁·q). Из правил умножения целых чисел следует, что произведение двух целых чисел есть целое число, тогда равенство a=b₁·(q₁·q) указывает на то, что b₁ является делителем числа a. Учитывая полученные выше неравенства 1<b₁<b, мы получаем противоречие условию, что b – наименьший положительный и отличный от единицы делитель числа a.

Теперь мы можем доказать, что простых чисел бесконечно много.

Теорема.

Простых чисел бесконечно много.

Доказательство.

Предположим, что это не так. То есть, предположим, что простых чисел всего n штук, и эти простые числа есть p₁, p₂, …, p_n. Покажем, что мы всегда можем найти простое число, отличное от указанных.

Рассмотрим число, p равное p₁·p₂·…·p_n+1. Понятно, что это число отлично от каждого из простых чисел p₁, p₂, …, p_n. Если число p — простое, то теорема доказана. Если же это число составное, то в силу предыдущей теоремы существует простой делитель этого числа (обозначим его p_n+1). Покажем, что этот делитель не совпадает ни с одним из чисел p₁, p₂, …, p_n.

Если бы это было не так, то по свойствам делимости произведение p₁·p₂·…·p_n делилось бы на p_n+1. Но на p_n+1 делится и число p, равное сумме p₁·p₂·…·p_n+1. Отсюда следует, что на p_n+1 должно делиться второе слагаемое этой суммы, которое равно единице, а это невозможно.

Так доказано, что всегда может быть найдено новое простое число, не заключающееся среди любого количества наперед заданных простых чисел. Следовательно, простых чисел бесконечно много.

Итак, в силу того, что простых чисел бесконечно много, при составлении таблиц простых чисел всегда ограничивают себя сверху каким-либо числом, обычно, 100, 1 000, 10 000 и т.д.

Жизнь

Эратосфен, сын Аглаоса, родился в 276 г. до н.э. в Кирене . Теперь часть современной Ливии , Кирена была основана греками несколько веков назад и стала столицей Пентаполиса (Северная Африка) , страны , состоящей из пяти городов: Кирены, Арсинои , Береники , Птолемея и Аполлонии . Александр Великий завоевал Кирену в 332 г. до н.э., и после его смерти в 323 г. до н.э. ее правление перешло к одному из его полководцев, Птолемею I Сотеру , основателю Птолемеевского царства . При Птолемеях экономика процветала, в основном за счет экспорта лошадей и сильфия , растения, которое использовалось в качестве приправ и лекарств. Кирена стала местом культивирования, где расцветали знания. Как и любой молодой грек того времени, Эратосфен учился в местной гимназии , где он изучал бы физические навыки и социальный дискурс, а также чтение, письмо, арифметику, поэзию и музыку.

Эратосфен учение в Александрии по Бернардо Строцци (1635)

Эратосфен отправился в Афины для продолжения учебы. Там его основатель Зенон из Citium преподавал стоицизму философские лекции о добродетельной жизни. Затем он учился у Аристо Хиосского , который руководил более циничной философской школой. Он также учился под руководством главы Платонической академии , которым был Аркесилай Питанский . Его интерес к Платону привел к тому, что он написал свою первую научную работу « Платоникос» , исследуя математические основы философии Платона. Эратосфен был человеком многих взглядов и исследовал искусство поэзии при Каллимахе . Он писал стихи: одно в гекзаметрах под названием « Гермес» , иллюстрирующее историю жизни бога; и другой в элегии , названный Эригон , описывающий самоубийство афинской девушки Эригоны (дочери Икария) . Он написал « Хронографии» — текст, в котором с научной точки зрения указаны важные даты, начиная с Троянской войны . Эта работа была высоко оценена за точность. Позже Георгию Синчеллу удалось сохранить из хронографий список 38 царей египетских Фив . Эратосфен также написал « Олимпийские победители» , хронологию победителей Олимпийских игр . Неизвестно, когда он писал свои произведения, но они подчеркнули его способности.

Эти произведения и его великие поэтические способности привели фараона Птолемея III Эвергета к поиску места его библиотекарем в Александрийской библиотеке в 245 году до нашей эры. Эратосфен, которому тогда было тридцать, принял приглашение Птолемея и отправился в Александрию, где прожил всю оставшуюся жизнь. Примерно через пять лет он стал главным библиотекарем — должность, которую ранее занимал поэт Аполлоний Родий . В качестве главы библиотеки Эратосфен обучал детей Птолемея, в том числе Птолемея IV Филопатора, который стал четвертым фараоном Птолемея. Он расширил фонды библиотеки: в Александрии все книги нужно было сдавать для тиражирования. Было сказано, что они были скопированы настолько точно, что невозможно было сказать, вернула ли библиотека оригинал или копию. Он стремился поддержать репутацию Александрийской библиотеки, несмотря на конкуренцию со стороны Пергамской библиотеки . Эратосфен создал целый раздел, посвященный исследованию Гомера, и приобрел оригинальные произведения великих трагических драм Эсхила , Софокла и Еврипида .

Эратосфен внес несколько важных вкладов в математику и науку и был другом Архимеда . Около 255 г. до н.э. он изобрел армиллярную сферу . В О круговых движениях небесных тел , Клеомед приписывал ему рассчитав окружность Земли около 240 г. до н.э., с высокой точностью.

Эратосфен считал, что в каждой нации есть и хорошее, и плохое, и критиковал Аристотеля за то, что он утверждал, что человечество разделено на греков и варваров , а также за то, что он утверждал, что греки должны сохранять свою расовую чистоту. В возрасте около 195 г. до н.э. он заболел офтальмией и ослеп. Утрата способности читать и наблюдать за природой мучила его и подавляла, заставляя добровольно морить себя голодом. Он умер в 194 г. до н.э. в возрасте 82 лет в Александрии.

Различные оптимизации решета Эратосфена

Самый большой недостаток алгоритма — то, что он «гуляет» по памяти, постоянно выходя за пределы кэш-памяти, из-за чего константа, скрытая в , сравнительно велика.

Кроме того, для достаточно больших узким местом становится объём потребляемой памяти.

Ниже рассмотрены методы, позволяющие как уменьшить число выполняемых операций, так и значительно сократить потребление памяти.

Просеивание простыми до корня

Самый очевидный момент — что для того, чтобы найти все простые до , достаточно выполнить просеивание только простыми, не превосходящими корня из .

Таким образом, изменится внешний цикл алгоритма:

for (int i=2; i*i<=n; ++i)

На асимптотику такая оптимизация не влияет (действительно, повторив приведённое выше доказательство, мы получим оценку , что, по свойствам логарифма, асимптотически есть то же самое), хотя число операций заметно уменьшится.

Решето только по нечётным числам

Поскольку все чётные числа, кроме , — составные, то можно вообще не обрабатывать никак чётные числа, а оперировать только нечётными числами.

Во-первых, это позволит вдвое сократить объём требуемой памяти. Во-вторых, это уменьшит число делаемых алгоритмом операций примерно вдвое.

Уменьшение объёма потребляемой памяти

Заметим, что алгоритм Эратосфена фактически оперирует с битами памяти. Следовательно, можно существенно сэкономить потребление памяти, храня не байт — переменных булевского типа, а бит, т.е. байт памяти.

Однако такой подход — «битовое сжатие» — существенно усложнит оперирование этими битами. Любое чтение или запись бита будут представлять из себя несколько арифметических операций, что в итоге приведёт к замедлению алгоритма.

Таким образом, этот подход оправдан, только если настолько большое, что байт памяти выделить уже нельзя. Сэкономив память (в раз), мы заплатим за это существенным замедлением алгоритма.

В завершение стоит отметить, что в языке C++ уже реализованы контейнеры, автоматически осуществляющие битовое сжатие: vector<bool> и bitset<>. Впрочем, если скорость работы очень важна, то лучше реализовать битовое сжатие вручную, с помощью битовых операций — на сегодняшний день компиляторы всё же не в состоянии генерировать достаточно быстрый код.

Блочное решето

Из оптимизации «просеивание простыми до корня» следует, что нет необходимости хранить всё время весь массив . Для выполнения просеивания достаточно хранить только простые до корня из , т.е. , а остальную часть массива строить поблочно, храня в текущий момент времени только один блок.

Пусть — константа, определяющая размер блока, тогда всего будет блоков, -ый блок () содержит числа в отрезке . Будем обрабатывать блоки по очереди, т.е. для каждого -го блока будем перебирать все простые (от до ) и выполнять ими просеивание только внутри текущего блока. Аккуратно стоит обрабатывать первый блок — во-первых, простые из не должны удалить сами себя, а во-вторых, числа и должны особо помечаться как не простые. При обработке последнего блока также следует не забывать о том, что последнее нужное число не обязательно находится в конце блока.

Приведём реализацию блочного решета. Программа считывает число и находит количество простых от до :

const int SQRT_MAXN = 100000; // корень из максимального значения N
const int S = 10000;
bool nprimeSQRT_MAXN, blS;
int primesSQRT_MAXN, cnt;
 
int main() {
 
	int n;
	cin >> n;
	int nsqrt = (int) sqrt (n + );
	for (int i=2; i<=nsqrt; ++i)
		if (!nprimei) {
			primescnt++ = i;
			if (i * 1ll * i <= nsqrt)
				for (int j=i*i; j<=nsqrt; j+=i)
					nprimej = true;
		}
 
	int result = ;
	for (int k=, maxk=nS; k<=maxk; ++k) {
		memset (bl, , sizeof bl);
		int start = k * S;
		for (int i=; i<cnt; ++i) {
			int start_idx = (start + primesi - 1)  primesi;
			int j = max(start_idx,2) * primesi - start;
			for (; j<S; j+=primesi)
				blj = true;
		}
		if (k == )
			bl = bl1 = true;
		for (int i=; i<S && start+i<=n; ++i)
			if (!bli)
				++result;
	}
	cout << result;
 
}

Асимптотика блочного решета такая же, как и обычного решета Эратосфена (если, конечно, размер блоков не будет совсем маленьким), зато объём используемой памяти сократится до и уменьшится «блуждание» по памяти. Но, с другой стороны, для каждого блока для каждого простого из будет выполняться деление, что будет сильно сказываться при меньших размерах блока. Следовательно, при выборе константы необходимо соблюсти баланс.

Как показывают эксперименты, наилучшая скорость работы достигается, когда имеет значение приблизительно от до .

Улучшение до линейного времени работы

Алгоритм Эратосфена можно преобразовать в другой алгоритм, который уже будет работать за линейное время — см. статью «Решето Эратосфена с линейным временем работы». (Впрочем, этот алгоритм имеет и недостатки.)

Что открыл Эратосфен в географии

Для своих размышлений и заключений древнегреческий философ употребил термин «география» (дословно: «землеописание»). Накопленный опыт и всесторонняя начитанность помогли ему составить общую картину земной поверхности.

Он высказал предположения о световом дне, его изменениях и отличиях в разных точках мира. Эратосфен измерил земной шар посредством деления участков на сектора. Его метод впоследствии преобразовался в концепцию параллелей и меридианов.

В своих исследованиях эллин пришел к выводу: если добраться до Гибралтара, а после плыть строго на запад, море приведет к берегам Индии. 

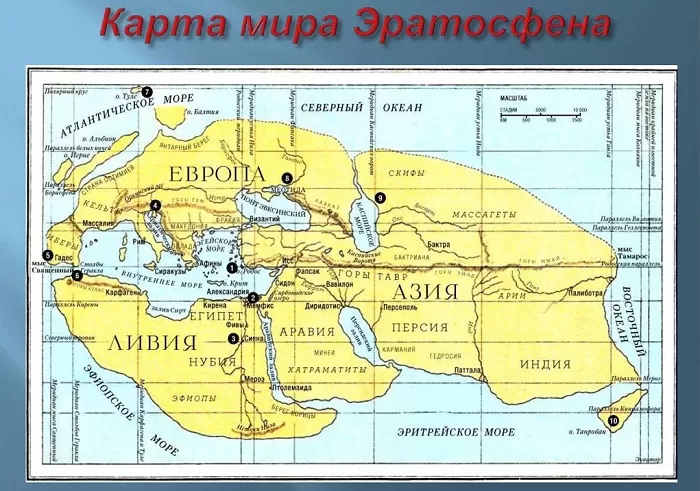
По итогам научных трудов Эратосфеном была составлена карта мира. И пусть она не совсем похожа на современные высокоточные фото Земли, для античного времени это было значительное открытие.

Отец географии установил точное положение крупных городов своего времени, островов и материков относительно друг друга, рассчитал их примерное положение на поверхности планеты.

https://youtube.com/watch?v=iIFCfs1f-Cg

Литература[править | править код]

• Античная география. М., 1953.
• Бобынин В. В. Эратосфен // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Дитмар А.Б. Родосская параллель: Жизнь и деятельность Эратосфена. — М.: Мысль, 1965. — 72 с.
• Колчинский И.Г., Корсунь А.А., Родригес М.Г. Астрономы: Биографический справочник. — 2-е изд., перераб. и доп. — Киев: Наукова думка, 1986. — 512 с.

На иностранных языках

• Aujac G. Eratosthène de Cyrène, le pionier de la geographie. — Paris: Édition du CTHS, 2001. — 224p.
• Diller A. Geographical Latitudes in Eratosthenes, Hipparchus and Posidonius // Klio. — 1934. — Bd. 27. — Heft 3. — S. 258—269.
• Dutka J. Eratosthenes’ measurement of the Earth reconsidered. Archive for History of Exact Sciences, 46, 1993, p. 55-64.
• Fraser P. M. Ptolemaic Alexandria. — Oxford: Clarendon Press, 1972.
• Goldstein B. R. Eratosthenes on the measurement of the Earth // Historia Mathematica. — Vol. 11. — 1984. — P. 411—416.
• Rawlins D. Eratosthenes’ geodesy unraveled: was there a high-accuracy Hellenistic astronomy, Isis, 73, 1982, p. 259—265.
• Rawlins D. The Eratosthenes — Strabo Nile map. Is it the earliest surviving instance of spherical cartography? Did it supply the 5000 stades arc for Eratosthenes’ experiment?, Arch. Hist. Exact Sci, 26 (3), 1982, p. 211—219.
• Rawlins D. Eratothenes’s large earth and tiny universe. DIO, 14, 2008.
• Shcheglov D. A. Ptolemy’s System of Seven Climata and Eratosthenes’ Geography // Geographia Antiqua. — Vol. 13. — 2004 (2006). — P. 21-37.
• Thalamas A. La géographe d’Ératosthène. — Versailles, 1921.
• Wolfer E. P. Eratosthenes von Kyrene als Mathematiker und Philosoph. — Groningen-Djakarta, 1954.

Асимптотика

Докажем, что асимптотика алгоритма равна .

Итак, для каждого простого будет выполняться внутренний цикл, который совершит действий. Следовательно, нам нужно оценить следующую величину:

Вспомним здесь два известных факта: что число простых, меньше либо равных , приблизительно равно , и что -ое простое число приблизительно равно (это следует из первого утверждения). Тогда сумму можно записать таким образом:

Здесь мы выделили первое простое из суммы, поскольку при согласно приближению получится , что приведёт к делению на нуль.

Теперь оценим такую сумму с помощью интеграла от той же функции по от до (мы можем производить такое приближение, поскольку, фактически, сумма относится к интегралу как его приближение по формуле прямоугольников):

Первообразная для подынтегральной функции есть . Выполняя подстановку и убирая члены меньшего порядка, получаем:

Теперь, возвращаясь к первоначальной сумме, получаем её приближённую оценку:

что и требовалось доказать.

Более строгое доказательство (и дающее более точную оценку с точностью до константных множителей) можно найти в книге Hardy и Wright «An Introduction to the Theory of Numbers» (стр. 349).

Эратосфен

Эратосфен (ок. 275 – 194 до н.э.), один из
самых разносторонних ученых античности. Особенно прославили Эратосфена труды
по астрономии, географии и математике, однако он успешно трудился и в
области филологии, поэзии, музыки и философии, за что современники дали ему
прозвище Пентатл, т.е. Многоборец. Другое его прозвище, Бета, т.е. «второй»,
возможно, также не содержит ничего уничижительного: им желали показать, что
во всех науках Эратосфен достигает не высшего, но превосходного результата.

Эратосфен родился в Африке, в
Кирене. Учился сначала в Александрии, а
затем в Афинах у известных наставников, поэта Каллимаха, грамматика Лисания,
а также философов – стоика Аристона и платоника Аркесилая. Вероятно, именно
благодаря столь широкому образованию и разнообразию интересов ок. 245 до
н.э. Эратосфен получил от Птолемея III Эвергета приглашение вернуться в
Александрию, чтобы стать воспитателем наследника престола и возглавить
Александрийскую библиотеку. Эратосфен принял это предложение и занимал
должность библиотекаря вплоть до своей кончины. Его научные таланты
удостоились высокой оценки современника Эратосфена, Архимеда, который
посвятил ему свою книгу Эфодик (т.е. Метод).

Сочинения Эратосфена не сохранились, мы имеем от них лишь фрагменты.
Трактаты Эратосфена Удвоение куба и О среднем были посвящены решению
геометрических и арифметических задач, в Платонике он обращается к
математическим и музыкальным основам платоновской философии. Самым
знаменитым математическим открытием Эратосфена стало т.н. «решето», с
помощью которого находятся простые числа. Эратосфен является
основоположником научной географии. В его Географии в 3 книгах содержалась
история географических открытий, а также рассматривался ряд физических и
математических проблем, связанных с географией, включая указание на
сферическую форму Земли и описание ее поверхности.

Однако самым известным достижением Эратосфена в области географии был
изобретенный им способ измерения величины земного шара, изложению которого
был посвящен трактат Об измерении Земли. Здесь было описано впервые
отмеченное в науке одновременное наблюдение и проведение измерений в столь
отдаленных точках, как Александрия и Сиена (совр. Асуан, Египет). Хотя
остается спорным, получилось ли у Эратосфена в итоге 250 000 стадий
(согласно Клеомеду) или 252 000 (по сообщению Страбона и Теона Смирнского),
в любом случае этот результат замечателен – диаметр Земли оказывается всего
лишь на 80 км меньше, чем фактический полярный диаметр. В этой же работе
были рассмотрены и астрономические задачи, такие, как размер Солнца и Луны и
расстояния до них, солнечные и лунные затмения и продолжительность дня в
зависимости от географической широты.

Эратосфена можно считать также основателем научной хронологии. В своих
Хронографиях он пытался установить даты, связанные с политической и
литературной историей Древней Греции, составил список победителей
Олимпийских игр. В трактате О древней комедии, где анализировались
произведения афинских драматургов, Эратосфен выступил как литературный
критик и филолог. Эратосфен написал также поэму Гермес, повествующую о
рождении, подвигах и гибели бога, до нас дошли ее фрагменты. Другой короткий
эпос, Гесиод, посвящен смерти поэта и каре, постигшей его убийц. Эратосфен
написал также трактат Катастеризмы – описание созвездий и изложение
посвященных им мифов (сохранившееся сочинение под таким названием вызывает
сомнения в смысле подлинности). Эратосфену принадлежал еще ряд работ по
истории и философии, которые не сохранились.

Использованы материалы энциклопедии «Мир вокруг нас».

На страже знаний

Узнать о том, что открыл Эратосфен в географии, 7 классу будет интересно еще и потому, что этот ученый по праву считается одним из мужей, кто своими усилиями оформил целый ряд научных направлений и отраслей знаний, которые способствовали славе Александрийской библиотеки.

Например, именно при Эратосфене в библиотеке были созданы целые отделы, сотрудники которых занимались переписью и изучением великих греческих поэтов, таких как Эсхил, Софокл, Еврипид и, конечно, Гомер.

Столь широкий круг интересов и неудержимая энергия стали причиной присвоения Эратосфену нескольких почетных прозвищ, наиболее расхожими среди которых были «пятиборец», что указывало на его всестороннюю развитость, и «бета», которое свидетельствовало о глубочайшем почтении, которое современники испытывали к великому филологу, признавая за ним статус настолько высокий, что опережал его лишь Платон.

Что открыл Эратосфен: кратко

В историю, и не только научную, но и мировую, греческий математик, астроном и географ вошел как первый человек, который не только задался вопросом о размере Земли, но и как ученый, которому удалось на этот вопрос ответить.

Ко времени, когда Эратосфен стал юношей, в Александрии активно действовала Академия, выпускавшая универсальных мудрецов, знавших толк в многочисленных науках, истории и поэзии. Свое первое образование будущий исследователь Земли получил у одного из самых известных поэтов своего времени — Каллимаха. Надо сказать, что любовь к литературе Эратосфен пронес через всю жизнь, до последнего называя себя филологом.

Однако его вклад в науку не ограничивается только лишь филологическими штудиями, но распространяется также на географию, математику и музыку

Большое внимание ученый уделял географии Египта, в котором он провел большую часть жизни и где окончил свои дни

Библиография

• Эратостен де Кирена ( пер.  Жорди Памиас и Массана и Арно Цукер), Catastérismes , Les Belles Lettres, колл.  «Собрание университетов Франции. Греческий сериал »,2013
• Хорди Памиас, «  Катастрофы Эратосфена. Мифографические выборы и производство знания  », Revue des études grecques , t.  127, п о  1,2014 г., стр.  195-206 .
• Жермен Ойак, «  Эратосфен, первый текстовый редактор?  », Pallas, обзор древних исследований , п о  24,1977 г., стр.  3-24 .
• Джермейн Aujac, «  Астрономия и научная география в древней Греции  », Бюллетень Ассоциации Бюде , п о  32,Декабрь 1973 г., стр.  441-461 .
• Жермен Ойак, Эратосфен де Кирен, пионер географии: его измерение окружности Земли , Париж, 2001 г. ( Format , 39) ( ISBN  2-7355-0457-3 ) .
• Жермен Ойак, География в Древнем мире , Париж, сб.  »  Что я знаю?  «( N O  1598)1975 г., стр.  15-20 и 70-78 (о географии и карте Эратосфена)
• К. Кюссет и Х. Франгулис (редакторы), Эратостен , спортсмен знаний , Publications de Saint-Étienne, 2008 г.
• Поль Педеш, География греков , PUF, коллекция SUP, 1976.
• Пьер Дюгем , Система мира: История космологических учений от Платона до Коперника , т.  II, Пэрис, Герман и сын ,1914 г. , гл. IX , «Измерение Земли. Эратосфен
• Мари-Николя Булье и Алексис Чассанг ( режиссер ), «Эратосфен» из Универсального историко-географического словаря ,1878 г.( читайте в Wikisource )
  
• (en) Джеймс Эванс , История и практика древней астрономии , Oxford University Press, США,Октябрь 1998, 480  с. .
• (ru) Ирен Фишер , «  Другой взгляд на определения окружности Земли Эратосфеном и Посидонием  » , Ежеквартальный журнал Королевского астрономического общества , т.  16,Июнь 1975 г., стр.  152

Романы

• Тьерри Крузе , Эратосфен , Возраст человека , 2014
• Денис Гедж , Волосы Беренис , Сеуил , 2003
• Жан Ромен , Библиотекарь , Эпоха Человека, 2005
• Арно Шмидт , Enthymésis ou CJVH , Кристиан Бургуа , 1991